Materials


The classification of materials into metal, semi metal, semiconductors and insulators is usually done based on their band structure as shown in Fig. 1


Figure 1. Sketch of electron energy spectra in solids at a nonzero temperature.
Taken from quantum mechanics for engineers. http://www.eng.fsu.edu/~dommelen/quantum/style_a/pboxbt.html

One can see that in metals the upper occupied level is within a continuum while in insulator there is a large energetic gap between the top occupied level which is completely filled and the next level. In semiconductors (intrinsic) the finite temperature is enough to allow electrons to overcome this gap and partially filled the next level. Because there are now two unfilled bands the original “insulator” has turned into a “semiconductor”.
The unique properties of a semiconductor are:

  • It is an insulator at zero temperature but conduct at finite temperature.
  • The conductivity rises with temperature because of the increased number of conducting charges. This is in contrast to metals.
  • The density of charges in the partially filled band can be controlled using doping.

    • The concept of band structure is derived from the arrangement of the elements in the lattice that gives rise to delocalised electronic states. As a result, it is therefore highly sensitive to defects (such as impurities and crystallite boundaries). Fabrication of high-quality crystal, mainly silicon, is very expensive and is a primary obstacle for large area photovoltaics and circuitry. The costs are even higher when luminescent semiconductor crystals for LEDs are considered. An elegant solution is to use materials with intrinsic semiconductor behavior that is not related to their spatial configuration. An example of such class of materials are molecular semiconductors. In this class the “semiconducting behavior” is mostly inherent to the molecule it self with smaller effects due to three-dimensional structure. A huge advantage of such class of materials is the ability to engineer their electrical and optical properties by synthetic chemistry. As a result, this field is dominated by organic (carbon based) molecules due to the superb flexibility of organic chemistry.

    From atomic orbits to conjugation


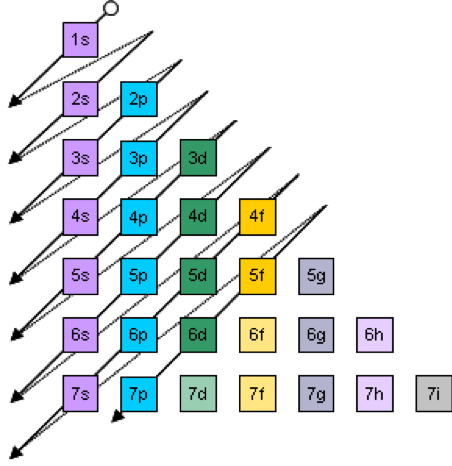
    The solution of the Schrödinger equation for an atom results in the concept of shells that are filled in accordance to the rule outlines in Fig. 2.


    Figure 2. Order of filling of atomic sub shells. Each shell can be occupied by 2(n2) electrons (n goes from 1 to 7) and each sub-shell has 2, 6, 10, 14.. electrons for the s, p, d, f sub-shells, respectively.

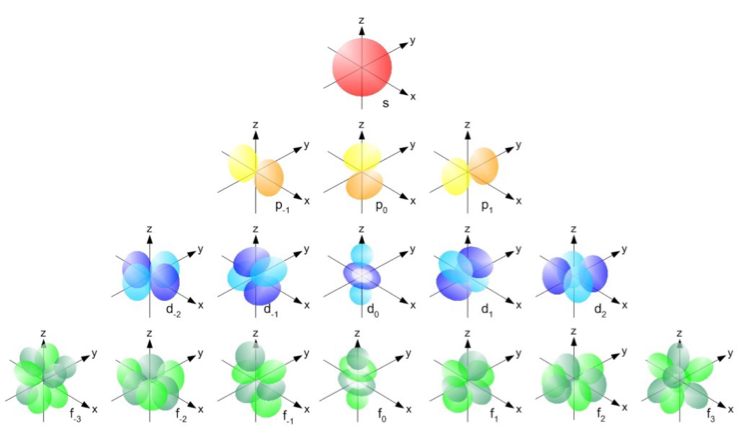
    Each atomic orbital has its own three-dimensional representation based on its angular momentum as depicted in Fig. 3.


    Figure 3.Three dimensional representation of electron probabilities for atomic orbitals.
    Taken from University of California, David ChemWiki Page. http://chemwiki.ucdavis.edu/

    Moving from an atom to a molecule there is a change in the orbitals due to the interaction between the atoms. The number of molecular orbits is identical to the number of atomic orbitals used to create them. Molecular orbitals are filled in accordance to their energy.

    Sp2 hybridization and the conjugation of carbon-carbo- bonds


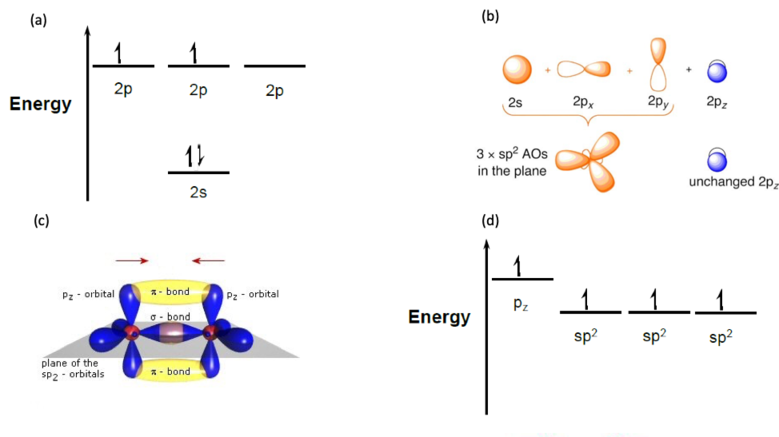
    As an example of the process of molecular orbit formation let us observe the 1,3 Butadiene molecule. In Fig 4. it is shown that level 2 of carbon is the outermost shell. This level is consisted of a filled 2s-level and partially filled 2p-level (4(a)). When the 1,3 Butadiene molecule is formed the three-dimensional configuration of the bonds is called sp2 hybridization (Fig. 4(b)) where the original atomic orbitals are mixed to create three new orbitals in the plane and one unchanged orbital that is perpendicular to it. This result of the hybridization and the formation of the molecule is that the three paired sp2 atomic orbitals (two with hydrogen and one with the adjacent carbon atom, Fig 4. (c)) has a lower energy then the unpaired pz orbital (Fig 4. (d)).

    Figure 4.From atomic to molecular orbits.

    The sp2 bonds are called σ bonds and have electrons that are localized to the bond. In contrast the two pz orbits form a weaker, delocalized bond called π bond. These bonds can extend over many carbon atoms, a process known as conjugation. The length of the conjugation is defined by the atoms and the three-dimensional configuration of the molecule.

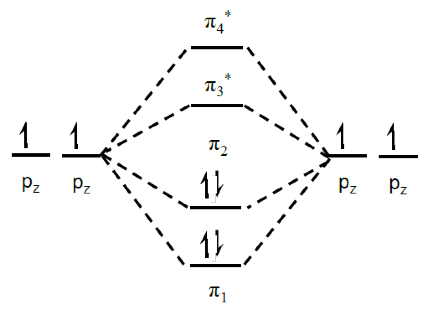
    The energy diagram of the possible pz electrons for the individual atoms and for the molecules is shown in Fig. 5.

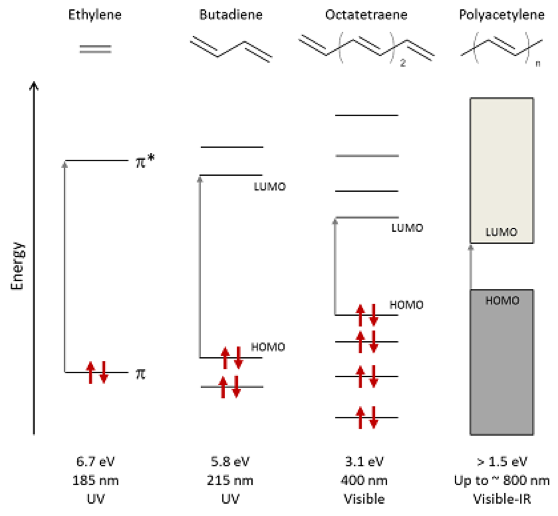
    Figure 5.Energy of AO and MO for the 1,3-Butadiene molecule.

    In this case, π2 is the Highest Occupied Molecular Orbital (HOMO) energy level and π3* is the Lowest unoccupied Molecular Orbital (LUMO) energy level. The splitting between the bonding, π, states and the antibonding, π* state is the equivalent to the energy gap in conventional semiconductors. As the number of molecules increases inner distance between the HOMO and LUMO decreases as can be seen in Fig. 6.

    Figure 6.Schematic of energy-level splitting and absorption in alkenes with increasing conjugation length, highlighting the lowest-energy optical transitions from HOMO to LUMO. The bandgap of polyacetylene depends on both the number of monomers n and the effective conjugation length in the polymer. Arrows represent spin-paired electrons.
    Taken from www.oe.phy.cam.ac.uk/research/materials/osemiconductors.html

    Organic vs inorganic semiconductors


  • Free electrons or polarons: Due to fact that organic semiconductor usually do not form a lattice their structure is more susceptible to perturbation. For example, charged carriers moving through an organic material are usually localized to a few carbon atoms, and so act as large perturbations to the local electronic structure. Polarization of the local medium (enhanced by low permittivity) and the breaking of local conjugation leads to geometric relaxation of the molecule. The fundamental charge carrier in organic materials is thus a polaron, a quasiparticle comprising the charge self-localized by its associated molecular distortion.

  • Transport of carriers is limited by “hopping” between molecules: The polaronic nature of the charged carriers combined with the lower degree of symmetry associated with these amorphous materials imply that migration of polarons between polymer chains or conjugated regions involves significant reorganization energy, reducing mobility. Therefore, this transport is referred to as inter-molecular “hoping” leading to low mobility compared to inorganic semiconductor with band conduction.

  • The dielectric constant of organic semiconductor, ε, is low: For example, εpentacene ~4 and in most organic materials 2-4 (can be modified by incorporating metals) whereas εsi ≈11.9. A high dielectric constant reduces the Coulomb attraction between excited electron-hole pairs to a few 10s of meV. These weakly bound e-h pairs (Wannier-Mott excitons) therefore undergo spontaneous dissociation into free charges via interactions with room-temperature lattice phonons. In contrast, materials with low dielectric constant, the Coulomb attraction is not strongly screened, leading to Frenkel-type excitons with binding energies around 0.1–1 eV. Dissociation of these excitons into free charge carriers is rarely spontaneous at room temperature (problematic for photovoltaics, potentially good for LEDs).

    • Sp2 Commonly used small molecules and polymeric materials



    Figure 7. Hole-transporting (a) and electron transporting (b) commonly used organic small molecules (Mishra, A. Bäuerle, P. Angew. Chem. Int. Ed. 2012 51 2020. . Hole-transporting (c) and electron transporting (d) commonly used polymers (Boudouris, B. W . Cuee. Opi. Chem. Eng. 2013 2 294.